Un tempo non esisteva calcolatrice di sorta e tutte le operazioni matematiche dovevano essere fatte a mano eseguendo direttamente le quattro operazioni fondamentali. Per i calcoli complessi si usavano i logaritmi i quali, trasformando le moltiplicazioni in addizioni, le divisioni in sottrazioni, le elevazione a potenza in moltiplicazioni e le estrazione di radici in divisioni, davano la possibilità di risolvere, sempre a mano, anche tali difficili problemi.
Erano le somme, soprattutto se relative a lunghissimi elenchi di numeri, che costituivano una questione molto seria.
La prima calcolatrice atta a risolverlo è stata, a notizia di chi scrive, la “sommatrice automatica” .Si tratta di un astuccio metallico delle dimensioni di circa 6 cm x 12 cm e dello spessore di qualche millimetro avente nel fronte una serie di fessure verticali ognuna delle quali è affiancata da una numerazione come rappresentato nella figura a fianco. Sopra ciascuna fessura e attraverso un piccolo foro circolare, è visibile la sottostante numerazione incisa su altrettante striscioline metalliche verticali che possono scorrere sempre in senso verticale. L’intera riga di fori circolari rappresenta il risultato. L’esecuzione di una somma ha luogo trascinando verso il basso ad una ad una e partendo da quella più a destra, le cifre costituenti i vari addendi tramite un piccolo accessorio cioè una specie di penna con punta metallica da inserire nelle fessure verticali e da tenere premuta contro un piccolo incavo appositamente ricavato nella sottostante strisciolina a lato di ciascuna cifra. Il risultato è visibile nella parte superiore entro la serie di piccoli fori circolari di cui si è detto. Ad esempio dovendo sommare tra di loro i due numeri 34 e 65, si riportano a zero tutte le striscioline facendole scorrere verso l’alto fino a portarle al fine corsa. Si inizia quindi a far scorrere verso il basso il quattro nella prima fessura e poi il tre del primo addendo in quella immediatamente a sinistra. Il risultato è il numero 34 leggibile in alto. Di seguito si porta in basso il numero cinque e quindi il sei. Risultato 99. Il funzionamento è chiaro: la strisciolina metallica interna scorrendo di volta in volta verso il basso rende leggibile il numero (da zero a nove) che si viene a trovare entro il foro circolare del risultato. Questo fintantocchè il totale di una stessa fessura non è superiore a nove. Allorchè la somma lo supera, l’operazione di trascinamento della strisciolina verso il basso viene impedita dal suo fine corsa ed allora, riscontrato tale inconveniente, senza spostare la penna dall’incavo se ne inverte la corsa e facendola scorrere verso l’alto con un percorso rigorosamente imposto dalla fessura di guida cioè con una breve deviazione finale verso sinistra. Ciò comporta due azioni: da una parte la sottrazione del complemento a 10 della cifra e, dall’altra l’aggiunta di una decina nella casella posta immediatamente a sinistra tramite la apposita dentellatura di cui è munita la strisciolina.
La cosa sarà meglio comprensibile con un esempio. Siano da sommare tra di loro i numeri 34 e 98. Inserito come nel precedente esempio, il numero 34 ed ottenutone il risultato corrispondente, si dia inizio a riportare in basso il numero 8 del secondo addendo. La cosa non è possibile perché la corsa della strisciolina si arresta. Allora si inverte il senso e si riporta verso l’alto e quindi verso sinistra il numero 8 andando ad interessare la colonna più a sinistra con spostamento verso il basso di una decina. In pratica si è sottratto da 34 il complemento a 8 cioè 2 ma si é aggiunto 10. Il risultato a questo punto è 42 cioè 34 – 2 +10. Resta ora inserire il numero 9 del secondo addendo. Anche questa operazione non và a buon fine. Occorre allora invertire il senso e, agendo verso l’alto, andare a interessare la colonna ancora più a sinistra cioè quella delle centinaia. In pratica si è sottratto da 42 il complemento a 90 cioè 10 ma si è aggiunto 100.Il risultato è ora pari a 132 cioè 42 -10 + 100.
Oltre a trattarsi di un sistema macchinoso e noioso non era possibile, come si capisce dal nome della macchinetta, eseguire nessuna altra operazione all’infuori della somma.
A un certo punto è apparsa in commercio la straordinaria Brunsviga manuale che risolveva tutti i problemi del genere e che è illustrata nella foto di fig. 2.
La macchina è composta da un rullo munito di più colonne di piolini (quadro delle impostazioni) che si possono spostare a mano verso il basso fino a leggere nella apposita riga il numero corrispondente. Fatto un giro con la manovella detto numero è riportato tale e quale nel sottostante quadro dei prodotti pronto a venire modificato in più nel caso di somma ed in meno per la sottrazione. Le due operazioni hanno luogo scrivendo in maniera del tutto analoga il secondo fattore e facendo ruotare rispettivamente in senso orario od antiorario a seconda si voglia fare la somma o la sottrazione dei due fattori. Si prosegue similmente fino ad aver battuto tutti gli addendi. Un altro indice ( quadro dei fattori ) segnala i numero di elementi sommati meno quelli sottratti. Tutta la procedura relativa ai riporti da una colonna all’altra avviene automaticamente grazie a una serie di ingranaggi e di levismi interni.
Per la moltiplicazione si deve usufruire di un’altra possibilità del rullo: il suo spostamento laterale effettuato tramite la leva di scorrimento che comporta un analogo spostamento sia del moltiplicando e sia del contatore superiore cioè del moltiplicatore.
Supponiamo di dover moltiplicare 455 per 23.
Si scrive con i piolini il n. 455 nel quadro delle impostazioni. Si fa girare la manovella per tre volte in senso orario per poi far scorrere il rullo verso sinistra mediante la apposita leva e quindi far girare due volte la manovella. La moltiplicazione è fatta e sarà possibile leggere il moltiplicando nel quadro delle impostazioni , il moltiplicatore nel quadro superiore dei fattori ed il risultato nello spazio inferiore cioè nel quadro dei prodotti.
Non esiste alcun modo per tener conto delle virgole e quindi tutte le operazioni devono essere fatte con numeri interi curando, per le somme e le sottrazioni, che le cifre impostate abbiano tutte lo stesso numero di decimali, all’occorrenza aggiungendo degli zeri dopo la virgola. Per la moltiplicazione il numero di decimali del risultato è dato dalla somma dei decimali dei due numeri da moltiplicare.
Più complessa l’esecuzione della divisione.
Scritto il dividendo con i piolini nel quadro delle impostazioni lo si riporta in quello inferiore detto quadro dei prodotti facendo girare una sola volta la monovella in senso orario. Si inserisce il divisore con i piolini e quindi si comincia a sottrarlo girando in senso antiorario la manovella. Nel quadro dei prodotti si legge allora il resto della sottrazione, L’operazione và ripetuta girando nello stesso modo la manovella finchè il resto rimane superiore al dividendo. Quando non lo è più, la sottrazione diventa impossibile e tale fatto viene annunciato da uno squillo di un campanello. Si torna allora nella precedente posizione tramite un giro orario di manovella per poi spostare il carrello al fine di allinearlo con una nuova casella. Tutta l’operazione viene ripetuta più volte con altrettanti spostamenti del carrello ed andando quindi ad interessare , ad ogni squillo, via via tutte le caselle del divisore. Si prosegue in questo modo fino ad esaurire tutto il resto. A questo punto sono leggibili nella parte inferiore cioè nel quadro dei prodotti il resto finale e nel contatore superiore (quadro dei fattori) il risultato della divisione, nel mentre il numero di decimali del risultato và calcolato manualmente e corrisponde alla differenza fra decimali del dividendo e quelli del divisore. L’operazione, vista ai nostri giorni in cui si trovano macchinette da due soldi in grado di compiere automaticamente operazioni matematiche di tutti i tipi, ivi compresa la determinazione dei valori naturali delle funzioni trigonometriche, fa veramente sorridere per la sua macchinosità. Ai tempi della nostra storia ha rappresentato invece un grande passo in avanti. Essa, nella realtà, è più difficile a spiegarsi che non a eseguirsi perchè, con una certa pratica, avviene del tutto automaticamente. Infatti una volta inserito il dividendo ed il divisore si tratta di far ruotare velocemente la manovella all’indietro fino allo squillo del campanello, spostare di una casella il carrello, riprendere a girare all’indietro e ripetere l’intera operazione fino allo squillo finale. L’intera azione risulta alla fine relativamente veloce.L’operazione di riporto a zero delle cifre è facilitata da apposite levette poste nel fianco della macchina.
La Brunswiga permetteva anche l’esecuzione della radice quadrata con un metodo molto intelligente ed arguto ma, anche in questo caso, risulta assai difficile spiegarne le modalità.
La radice viene così eseguita.
Si inserisce il numero da cui estrarre la radice nel quadro delle impostazione tramite i piolini e lo si divide mentalmente in gruppi di due cifre. L’operazione inizia operando nel gruppo più a sinistra e sottraendovi, cioè facendo girare all’indietro la manovella, di volta in volta i numeri dispari : prima 1, poi 3, poi 5, poi 7 e così via fintantocché il solito campanello non annuncia giunta la fine. Allora si torna indietro di un giro e si diminuisce il numero appena impostato e che non è più sottraibile dal resto, di una unità, si sposta il carrello verso destra e si inizia, a sottrarre, nel gruppo di due cifre immediatamente a desta, di nuovo ed uno di seguito all’altro, i numeri dispari. L’operazione và ripetuta fino ad esaurire tutte le cifre del resto. Nel contatore superiore (quadro dei prodotti) si legge allora il risultato mentre in quello inferiore (quadro dei fattori) il resto.
Anche in questo caso l’operazione risulta più facile di quanto non appaia dalla descrizione appena fatta. In pratica, inserito il primo numero, si tratta di sottrarvi via via 1, 3 , 5 ecc. ecc. spostando il carrello di una casella ogni qual volta suona il campanello.
Un esempio chiarirà meglio le operazione e potrà fornire anche la dimostrazione del procedimento.
Si debba ad esempio estrarre la radice quadrata del numero 104976. La prima coppia di numeri a sinistra è 10. Si inizierà allora a sottrarvi il numero 1 operando nella colonna sottostante al 10 medesimo. Dopo il primo giro all’indietro il resto (quadro dei prodotti) segnala 94976. Si sottrarrà allora il numero 3 ottenendo un resto di 64976, quindi il 5 ottenendo un resto pari a14976. Il successivo tentativo di sottrarre da 1 il numero 7 darà esito negativo segnalato dallo squillo. Si compie un giro in senso orario e si trasforma manualmente il numero 7 appena scritto ma non utilizzato perché non contenibile nel resto, nel numero immediatamente inferiore cioè il 6 . Si sposta il carrello verso destra e si comincia a sottrarre le solite cifre 1, 3, 5, 7 ecc. dal secondo gruppo di due cifre scrivendole di fianco al numero 6 di cui si è appena detto. In pratica si sottrae da 14976 dapprima il 61 ottenendo 8876, poi 63 ottenendo 2576. La successiva cifra pari a 65 non è più contenibile nel resto. Il campanello suona, si torna indietro di un giro, si trasforma il 5 in 4, si sposta il carrello verso destra e si inizia la nuova serie di numeri dispari. Il prossimo sottraendo sarà 641 con resto 1935, quindi 643 con resto 1292, quindi 645 con resto 647 e per ultimo 647 con resto zero. La radice è completa e nel contatore superiore (quadro dei fattori) si leggerà il risultato pari a 324 e che corrisponde al numero di giri fatti dal carrello nelle varie posizioni.
La dimostrazione del procedimento è data dal fatto che sottraendo di seguito uno all’altro i numeri dispari non si fa altro che sottrarre il quadrato della serie progressiva di cifre che compongono il risultato. Nell’esempio si sono via via sottratti 1 che è il quadrato di 1, 1+3 che è il quadrato di 2, 1+3+5 che è il quadrato di 3 (tre è la prima cifra del risultato). Si è poi sottratto il numero 100+300+500+61= 961 che è il quadrato di 31, poi 961+63=1024 che è il quadrato di 32 (32 sono le prime due cifre del risultato). Si è poi spostato il carrello e cominciato a sottrarre 102400+641=103041 cioè il quadrato di 321, poi 103041+643=103684 che è il quadrato di 322, poi 103684+645=104329 che è il quadrato di 323, infine 104329+647=104976 che è appunto il quadrato del risultato finale cioè 324. In altri termini tutta l’operazione è consistita nel ricercare via via per tentativi successivi ma non casuali quel numero che elevato al quadrato desse il numero iniziale di cui si ricercava la radice. Anche in questo caso l’operazione effettiva è più semplice di quanto non appaia dalla spiegazione. Si tratta, in effetti, di sottrarre in maniera progressiva la serie di numeri dispari a partire ogni volta da 1 salvo spostare il carrello quando la sottrazione diventa impossibile riducendo poi di una unità il numero impostato.
Chi ha costruito la prima Brunsviga, oltre ad una buona tecnica meccanica, doveva sicuramente possedere una grande immaginazione per scoprire un metodo, sia pur nella sua meccanosità, così intelligente di risolvere un problema, per quei tempi così difficile.
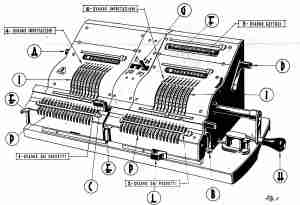
Il progresso nella costruzione delle calcolatrici meccaniche ha raggiunto, ad una certa data, livelli veramente elevati quando si è diffusa la calcolatrice manuale Brunsviga doppia che, a mio modo di vedere, rappresenta una somma di intelligenza. Si tratta di due calcolatrici manuali del tutto analoghe a quella prima descritta abbinate tra di loro e che possono funzionare sia girando ambedue nello spesso senso o nel senso contrario l’una rispetto all’altra a seconda della impostazione data dall’operatore nel mentre il contatore meccanico o numeratore che dir si voglia, è unico. In pratica la calcolatrice doppia è in grado di effettuare contemporaneamente due operazioni di somma, sottrazione, moltiplicazione o divisione, in funzione di un unico numeratore. Ad esempio si può moltiplicare, con una unica operazione, per 43 sia il numero 520 che il numero 88 ottenendo nei due registri (quadri dei prodotti) i due risultati rispettivamente 22360 e 3784. Ma la cosa straordinaria è rappresentata dal fatto che una volta opportunamente impostate le due calcolatrici, è possibile, agendo sul carrello e sulla manovella di rotazione, ricercare quella soluzione che dà, per ambedue le formule impostate, un unico risultato consentendo così di risolvere, in maniera semplice, problemi matematici che avrebbero, con le normali calcolatrici allora in uso, richiesto complicatissime procedure. Ciò può aver luogo ogni qualvolta esistono, come in matematica o in geometria accade assai frequentemente, due diverse formule che, partendo da dati diversi, portano al medesimo risultato. Si tratta in qualche modo di precorrere i tempi e cioè di una rudimentale applicazione del calcolo iterativo, comunemente usato nei moderni computer.
Come noto, ai nostri giorni, quando siamo in presenza di problemi particolarmente difficili da risolvere, si ricorre alla iterazione che consiste nell’iniziare il calcolo con una procedura approssimata e quindi affinare via via il risultato, sempre con procedure approssimate ma semplici. Ad ogni iterazione il computer confronta il nuovo risultato con quello precedente sospendendo le iterazioni non appena la differenza riscontrata rientra entro le tolleranze ammesse. Allo stesso modo con la calcolatrice doppia il risultato viene via via affinato fino ad ottenere, con la equiparazione di quello dell’una a quello dell’altra macchina che funziona in parallelo o in senso contrario, la risoluzione definitiva di problemi matematici complessi. Non si ritiene opportuno in questa sede descriverne in dettaglio le procedure, data la difficoltà che vi si incontrerebbe. Ci si limita ad indicare come, nella realtà , fossero in grado di dare, tenuto conto dei tempi di cui si discorre ed una volta imparate, velocità nei calcoli prima giudicate impensabili. Basterà qui dire che in ognuna delle due calcolatrici abbinate bisogna impostare i dati di una formula atta a dare il medesimo risultato fatta salva la necessità di tener conto dei segni matematici di ogni elemento mediante la regolazione del senso di rotazione dell’una macchina rispetto all’altra e del senso di rotazione assoluto della manovella. Il tutto codificato in regole precise del libretto di istruzioni che veniva fornito, in copia eliografica di un lucido redatto a mano libera, assieme alla machina e di cui si riporta, per darne un’idea di massima, un breve estratto nelle figure 3 e 4. Dalla sua lettura si capisce come la macchina sia stata utilizzata da chi scrive queste note, esclusivamente per calcoli topografici, per i quali essa presentava ottime performances. Il suo uso si estende però a calcoli di qualsiasi tipo fatta salva la difficoltà di conoscerne le regole, assai complicate ma necessarie per una efficace .utilizzazione delle peculiari caratteristiche. Ci si deve però rendere conto di quali erano le reali difficoltà che si incontravano allora nella esecuzione di calcoli oggi resi estremamente facili dai mezzi di calcolo di cui si può facilmente disporre. Occorre a tale riguardo accennare anche ad un’altra caratteristica dei calcoli topografici di quei tempi e cioè quella legata all’uso dei valori naturali delle funzioni trigonometriche la cui determinazione era un motivo in più per rendere le operazioni difficoltose. Ad esempio per determinare il valore, con una approssimazione spinta ad almeno otto decimali necessari per i calcoli topografici, del seno di un angolo dato in gradi, primi, secondi e decimi di secondo occorreva effettuare a mano l’interpolazione tra due dati, letti nel manuale relativo, ma che si riferivano ad angoli di valore arrotondato alla decina di secondi. L’operazione, facilitata da una tabella delle interpolazioni che era riportata sul fianco della pagina, presentava comunque una certa complessità e un discreto margine di errore.
In un secondo tempo le calcolatrici meccaniche vennero elettrizzate e quindi le stesse operazioni descritte erano eseguite, con la medesima sequenza, ma del tutto automaticamente. Era allora una vera comica vedere questo carrello, soprattutto nelle moltiplicazioni e nelle divisioni, che saltellava lateralmente a velocità impressionante.
La vera rivoluzione nel calcolo matematico si è avuta più tardi con l’avvento delle prime calcolatrici digitali e, subito dopo, di quelle tascabili programmabili. Queste ultime, pur consentendo di utilizzare solo pochi passi di programma (all’inizio erano solo 25) purtuttavia diedero una immediata percezione delle loro enormi possibilità, confermate poi dall’uscita di macchinette tascabili molto potenti e contemporaneamente da quell’autentico gioiello che fu il primo personal computer e cioè l’Apple secondo. Da allora è stato un susseguirsi di eclatanti novità fino a giungere, in breve tempo, ai moderni personal la cui rilevante potenza di calcolo assieme alla grande disponibilità di programmi applicativi permette di eseguire agevolmente calcoli matematici di ogni genere e non solo quelli. Descrivere le caratteristiche dei moderni personal esula totalmente dalle finalità della presente nota, pertanto la mia piccola storia delle calcolatrici finisce qui. Il tema delle calcolatrici in essa trattato è così vasto da richiedere, per una descrizione esaustiva, interi volumi. Ma lo scopo qui perseguito non è questo. Ho voluto semplicemente ricordare alcune caratteristiche delle calcolatrici meccaniche pensando sia bene non ne vada perduta la memoria per l’intelligenza e peculiarità che le caratterizzano e che ritengo di sicuro interesse scientifico nonchè atte a destare la curiosità dei lettori.