LA TOPOGRAFIA PRATICA DEGLI ANNI 50

 

1) PREMESSA

l progresso della tecnica topografica di questi ultimi anni è stato così notevole da provocare una vera rivoluzione nelle operazioni di campagna e nei relativi calcoli a tavolino.
Ne sono derivati l’abbandono di un cospicuo patrimonio di procedure con le quali si riusciva ad ottenere lusinghieri risultati anche con i mezzi relativamente modesti allora disponibili ed inoltre la loro irrimediabile perdita essendo fatalmente destinate ad entrare nell’oblio. Si cerca qui di scongiurare tale pericolo descrivendone gli aspetti curiosi ed intelligenti sperando, al tempo stesso, che tale loro caratteristica peculiare possa destare l’interesse dei lettori.
La trattazione è volutamente limitata alla parte pratica, operativa di alcune operazioni topografiche tralasciandone la teoria in quanto esula completamente dagli scopi di questo lavoro.

 

2)  LA MISURA DELLE  DISTANZE

La misura delle distanze, un tempo, rappresentava un problema di difficile soluzione in tutte le operazioni topografiche.
L’attrezzo più usato era allora il nastro metrico da 20 o da 50 metri in tela o in acciaio che poteva dare buoni risultati solo quando il terreno su cui si operava era pianeggiante oppure, abbinato con il filo a piombo, in presenza di dislivelli modesti. Negli altri casi era molto usata la coppia di triplometri muniti di bolla atta a garantirne la verticalità o l’orizzontalità. Si eseguiva la ben nota canneggiata cioè la sezione del terrreno con rilievo delle distanze in proiezione orizzontale e, quando necessario, anche dei dislivelli.

 

 

La canneggiata, completa degli opportuni riferimenti planimetrici di solito effettuati tramite allineamenti, squadro semplice o graduato e nastro metrico, ha costituito per decenni la modalità più adottata per rilevare i terreni ma, soprattutto per quanto riguarda la misura della distanza, di cui tratta questo capitolo, i risultati erano modesti.
In tale settore, e, più in generale, nei rilievi topografici, un notevole balzo in avanti é stato compiuto con l’uso del tacheometro e del più preciso teodolite.
Caratteristica saliente di questi strumenti era una grande precisione nella misura degli angoli nel mentre per quanto riguarda quella delle distanze, ottenuta mediante lettura dei tre fili del reticolo su una comune stadia verticale da 4 metri, i risultati erano assai modesti essendo possibile un errore di circa lo 0.2% della lunghezza in gioco nel mentre l’estesa di ogni misura non poteva superare i 200 m.
In tutti i casi in cui era richiesta una maggior precisione era necessario ricorrere a particolari metodologie mediante le quali la misura delle distanze era ricavata esclusivamente da quella angolare essendo, come detto, soltanto quest’ultima la determinazione che gli strumenti allora disponibili potevano effettuare con grande precisione. Ne é derivata una fioritura di artifici riguardanti sia il lavoro di campagna sia il calcolo a tavolino sui quali vale la pena di soffermarsi per gustarne appieno l’intelligenza.
La difficoltà incontrata nella misura delle distanze imponeva l’adozione di regole particolari sopratutto nelle operazioni topografiche inerenti la costruzione di grandi opere, ad esempio gli impianti idroelettrici. In questo caso il primo intervento consisteva nella creazione di una rete di caposaldi altimetrici e planimetrici che costituivano i riferimenti fissi per i tracciati. Nonostante si fosse in presenza di opere molto estese, pur tuttavia il relativo campo topografico di lavoro era ristretto se paragonato a quello della cartografia nazionale e internazionale e, in quanto tale, consentiva di trascurare le problematiche dovute alla sfericità terrestre, potendo invece operare in piano e quindi utilizzare le normali regole della trigonometria piana e della geometria analitica. Un’altra ragione per consigliare detta metodologia va ricercata nella necessità di usare dimensioni reali in quanto destinate a due funzioni la cui approssimazione ammissibile era estremamente contenuta: il tracciamento e la contabilizzazione delle opere. Gli elementi topografici dovevano quindi essere scevri da ogni alterazione e quindi anche di quelle normalmente usate nella topografia classica per rappresentare nel piano la superficie elissoidica del suolo, primo tra tutti il modulo di deformazione lineare correntemente applicato nella proiezione di Gauss-Boaga.
Il primo problema da affrontare, quando si iniziava la realizzazione della rete trigonometrica fondamentale era la misura delle basi, di solito in numero di due per ciascuna rete e che, come sarà spiegato più avanti, costituivano l’elemento di partenza e quello di arrivo della rete di caposaldi. Dalla loro precisione dipendeva, pertanto, l’esattezza dell’intera rete
Tra i molti sistemi descrivo quello basato sulla stadia orizzontale in invar che ho personalmente avuto modo di usare per la misura delle basi in argomento . La stadia consisteva in una coppia di mire nere su sfondo bianco di forma triangolare tenute rigorosamente ad una distanza di 2 metri esatti una dall’altra da un filo in invar, metallo che ha la caratteristica di conservare inalterata nel tempo la sua lunghezza anche al variare della temperatura ambientale.
La base da misurare consisteva in un rettifilo della lunghezza di circa 700-800 metri scelto in posizione opportuna su terreno orizzontale e materializzato in posto da una serie di picchetti con chiodini perfettamente allineati e posti ad un interasse di una trentina di metri. Fatta stazione sul picchetto n. 1 con il teodolite e posta la stadia invar in quello n. 2 dopo averla messa in bolla ed orientata tramite l’apposito mirino, veniva letto, seguendo rigorosamente le regole di cui al seguente capitolo 3), l’angolo sotteso per avere, tramite un semplice calcolo o le tabelle di cui era corredata la stadia, la distanza esatta che intercorreva tra i due picchetti. Il teodolite veniva poi spostato sul picchetto n. 3 e, fatta ruotare la stadia di 180 gradi attorno al suo asse, ripetuta la lettura dell’angolo e la determinazione della misura del secondo tratto. Era la volta, subito dopo, di ruotare il teodolite di 180 gradi attorno al suo asse verticale per poter rilevare, in maniera analoga, la successiva lunghezza del terzo tratto. L’intera operazione veniva ripetuta spostando lo strumento via via su tutti i picchetti di numero dispari e la stadia in quelli pari fino ad esaurire l’estesa totale della base. La lunghezza complessiva della base veniva determinata una seconda volta facendo stazione sui picchetti di numero pari e con stadia in invar piazzata in quelli dispari. La misura definitiva era data dalla media aritmetica dei due valori così ottenuti.
E’ impressionante la diversità che sussiste con una misura dello stesso tronco di 700/800 metri eseguita ai nostri giorni che, grazie all’uso del diffusissimo distanziometro a raggi infrarossi, non richiederebbe che pochi minuti di lavoro! Ma la cosa ancora più eclatante é data dal fatto che la base nelle moderne triangolazioni, a bella posta diventate trilaterazioni, non esiste più in quanto é normale effettuare la misura diretta delle distanze da un trigonometrico all’altro, il che, oltre ad una grande semplificazione delle procedure, assicura risultati ancora migliori di quelli, pur sempre ottimi, che si raggiungevano un tempo!

 

3) LA LIVELLAZiONE

La determinazione delle quote altimetriche tramite livellazione geometrica è forse la sola operazione topografica che in questi ultimi anni ha subito poche trasformazioni. L’unico miglioramento oggi presente è quello dell’automatismo che garantisce l’orizzontalità del piano di mira del livello nel mentre nei vecchi strumenti essa doveva essere ottenuta manualmente portando a coincidere le due semi-immagini della bolla.
Aggiungerei che, in questo particolare settore, la precisione era senza dubbio più elevata nei vecchi livelli con bolla a riflessione di immagine rispetto a quella degli attuali strumenti automatici.
Mi preme segnalare come tutte le determinazioni altimetriche mediante livellazione venissero eseguite tassativamente in doppio modo cioè in andata e ritorno oppure con percorso ad anello chiuso al fine di consentire una sicura verifica dei risultati e di effettuare la compensazione degli errori di chiusura.
Nelle operazioni importanti l’assenza di errori grossolani era assicurata in doppio modo grazie ad una determinazione totalmente indipendente da quella in oggetto e cioé tramite la livellazione trigonometrica, come indicato in dettaglio nel cap. 9), il che costituiva un ulteriore fattore di garanzia di buona qualità delle operazioni topografiche eseguite.

 

 

Merita di essere qui ricordato, per la praticità che lo caratterizzava, il livelletto di Abney un tempo molto usato per misure altimetriche nelle quali non fosse richiesta una grande precisione. Consisteva in un cannocchiale privo di lenti attraverso il quale era possibile vedere, fianco a fianco, la bolla della livella inclinabile a piacere e la mira e quindi eseguire la livellazione ed anche tracciare livellette con pendenza prefissata.

 

4) I PRIMI STRUMENTI AUTOMATICI

Oltre ai livelli automatici cui si é fatto cenno al capitolo precedente, nei primi anni 50 sono apparsi i tacheometri autoriduttori Wild RDS e RDH che, tramite dispositivi esclusivamente meccanici, consentivano di raggiungere risultati ragguardevoli: la lettura diretta alla stadia della distanza orizzontale e del dislivello tra stazione e punto battuto.

 

 

Il primo dei due strumenti era un comune tacheometro che, in luogo del normale reticolo con tre trattini fissi, era munito di un reticolo che, tramite organi meccanici, variava in funzione dell’inclinazione sull’orizzonte del cannocchiale e quindi dava direttamente le due misure lette su una comune stadia verticale a 4 m. Si otteneva una grande facilitazione nel lavoro ma permanevano, per quanto riguarda la precisione dei risultati, gli stessi inconvenienti del tacheometro tradizionale e sopratutto la scarsa precisione delle distanze misurate. Tali problemi erano invece brillantemente risolti dal RDH, un geniale e complicatissimo apparecchio il quale, tramite un doppio sistema ottico, sovrapponeva l’estremità destra della speciale stadia orizzontale piazzata tramite cavalletto sul punto da rilevare, a quella di sinistra.

 

Sopra il cannocchiale si trovava la vite micrometrica, visibile nella foto allegata dove è contrassegnata col n. 2, agendo sulla quale si poteva far ruotare uno dei due sistemi ottici provocando lo scorrimento di un’immagine sull’altra e quindi leggere la distanza orizzontale ed il dislivello in maniera del tutto analoga ad una normale lettura del nonio. Ovviamente tutto l’automatismo agiva, tramite un complicato meccanismo automatico, in funzione dell’inclinazione del cannocchiale rispetto all’orizzonte in modo da dare, con grande precisione, la distanza ridotta all’orizzonte ed il dislivello. Si può capire come quest’ultimo strumento costituisse un notevole balzo in avanti nella tecnica della topografia frenato però dal suo elevatissimo costo d’acquisto e, soprattutto, dalla lentezza di uso. Ogni battuta al punto da rilevare richiedeva infatti la posa in opera e la messa in bolla, su di esso, della stadia tramite l’apposito treppiede con un’operazione lunga e, nei terreni accidentati od in presenza di ostacoli, di difficile attuazione. Ne derivava un rilievo del terreno tutt’altro che “celerimetrico” il che ne ha, in definitiva, decretato la scarsissima diffusione.

 

5) LA MISURA DEGLI ANGOLI

Lo strumento più semplice che veniva usato in operazioni di modesta entità e precisione era lo squadro, in origine costituito da un cilindro in lamierino munito di un sistema di traguardi formato da coppie di fessure verticali contrapposte, alcune dotate in mezzeria di un sottile filo.Il suo uso, un tempo limitato soltanto al tracciamento di angoli di 90 gradi, con la applicazione di un cerchio graduato ed anche della bussola, è stato esteso alla misura di angoli in genere.

 

Molto usato, per il solo tracciamento di angoli a 90 e 45 gradi, lo squadro a prismi il quale, piazzato nel vertice dell’angolo da tracciare e tramite un sapiente gioco delle facce speculari dell’ottica, creava un’immagine sovrapposta delle due paline di direzione dei due lati dell’angolo consentendo di giungere al risultato in maniera rapida e precisa. Lo squadro a prismi presentava l’altra utile caratteristica di poter tracciare un punto intermedio di un rettifilo materializzato sul posto da due paline od oggetti inaccessibili. Esso infatti dava all’operatore la visione sovrapposta delle due paline di inizio e fine rettifilo consentendo una agevole identificazione del punto intermedio perfettamente allineato con gli altri due.

 

 

 

Gli strumenti topografici che consentivano di effettuare misure angolari di grandissima precisione erano il tacheometro e sopratutto il teodolite con i quali era possibile ottenere ottimi risultati sfruttando razionalmente tale loro fondamentale caratteristica e tramite una oculata organizzazione del lavoro.
Non si può evitare un sia pur minimo accenno a quello che, per le sue straordinarie doti di praticità e precisione é stato il re dei teodoliti : il Wild T2. Per avere un’idea della cura con cui era costruito basterà dire che per la lettura dei cerchi, finemente scolpiti in vetro, esisteva un sistema ottico che affiacava due parti diametralmente opposte del cerchio nel mentre una apposita vite micrometrica consentiva di farle scorrere una rispetto all’altra fino a farle coincidere e leggere quindi i decimi ed i centesimi di grado. L’angolo corrispondeva alla media fra i due valori diametralmente opposti del cerchio contribuendo a migliorare la già notevole bontà dei risultati.

 

Da segnalare anche il teodolite Kern DKMQ1 il quale alla grande precisione nella misura degli angoli univa la caratteristica, assai apprezzata quando si operava in alta montagna, di grande facilità di trasporto per la sua notevole leggerezza dovuta non solo alle contenute dimensioni ma anche alla singolare costituzione. Basterà far notare l’assenza delle normali ed ingombranti viti di elevazione sostituite da leggere viti a corsa breve e da una intelligente testa snodabile del treppiede in alluminio che, essendo collegata all’asta verticale di posizionamento, garantiva di per sé una prima verticalità dello strumento compatibile con la breve corsa delle suddette viti.
Stupefacente anche il sistema di lettura dei cerchi graduati. Come risulta dalla foto allegata ogni trattino inciso nel cerchio ad un intervallo di 20 primi viene, tramite un sistema ottico, affiancato al corrispondente trattino diametralmente opposto in modo da far apparire delle coppie di segni molto ravvicinati. Tramite un micrometro ottico, la cui rotazione fornisce il valore dei primi,dei decimi e dei centesimi di grado, si sposta l’indice fisso fino a portarlo esattamente sulla mezzeria dei due trattini. Agendo in questo modo si fà la media delle due letture del cerchio diametralmente opposte e quindi eliminando eventuali errori di eccentricità dell’alidada.

 

 

 

 

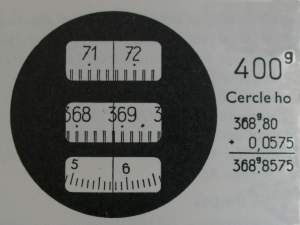
6) LA POLIGONALE

La poligonale costituiva l’ossatura di base della maggior parte del rilievo di aree aventi una estesa superiore ad 400 metri circa oppure con visibilità resa difficile dalla presenza di ostacoli e da eseguirsi sia con la celerimensura e sia tramite le già descritte canneggiate e squadro.
La poligonale dei rilievi celerimetrici era composta da una serie di lati ciascuno di lunghezza inferiore a 200 metri costituenti un percorso aperto o chiuso su sè stesso oppure su punti di coordinate note al fine di poter effettuare la compensazione degli errori seguendo le regole classiche. La misura degli angoli intercorrenti tra un lato e l’altro era fatta in duplice modo con strumento diritto e capovolto al fine di evitare gli errori per cattiva verticalità dello strumento o errata lettura del cerchio orizzontale. La distanza tra i vertici era data dalla media aritmetica dei due valori letti in andata e ritorno sulla stadia verticale.

 

7) IL RILIEVO CELERIMETRICO

Era quella in argomento la modalità comunemente usata nella maggior parte dei rilievi e che merita una approfondita disamina.
Le funzioni da svolgere in quel contesto erano molteplici e variegate, da esse dipendeva la qualità del prodotti finale e la durata del lavoro. Occorreva innanzitutto operare la semplificazione della configurazione del terrreno trascurandone gli elementi poco rappresentativi e scegliendo accuratamente i punti atti a definirne fedelmente l’andamento. I punti da rilevare risultavano comunque in numero sempre elevato il che ha portato alla adozione di tecniche speciali volte ad abbreviare al massimo i tempi di esecuzione del lavoro di campagna e di quello a tavolino. Tra di esse segnalo le particolarissime modalità correntemente adottate dal sottoscritto per la più onerosa tra tutte le operazioni e cioè per la lettura della stadia.

Come noto gli elementi da determinare per ciascuno dei punti da battere erano cinque.
Tra di essi erano i fili del reticolo a condizionare pesantemente l’esecuzione del lavoro di campagna in quanto, dovendo essere letti alla stadia mantenuta perfettamente verticale sul punto da rilevare, impegnavano il canneggiatore per tutto il tempo necessario per posizionarsi sul punto e per restarvi durante la lettura. Invece gli altri due elementi, cioè il cerchio orizzontale e quello verticale, potevano essere letti anche più tardi ed indipendentemente dall’opera del canneggiatore stesso che risultava quindi libero di spostarsi, nel frattempo, nel nuovo punto. In altri termini la velocità di esecuzione del rilievo celerimetrico dipendeva, in buona parte, dalla rapidità di lettura della stadia. Sono ben note le caratteristiche delle tre letture ai fili del reticolo. La differenza tra superiore ed inferiore dava la distanza inclinata da ridurre, con successivo calcolo, all’orizzonte. Il filo medio, oltre a servire per il controllo della lettura, entrava nel calcolo della quota del punto. Per esempio immaginiamo che le tre letture fossero, nell’ordine 1.20, 1.40, 1.60. La differenza 1.60-1.20, moltiplicata per il coefficiente 100, cioè 40.00, costituiva la distanza inclinata mentre 1.20, oltre fornire la prova di corretta lettura in quanto corrispondente esattamente alla media aritmetica degli altri due valori, dava l’altezza da sottrarre dalla quota del piano di mira per ottenere quella del suolo. In campagna la stima e la trascrizione a mano delle tre letture nonché un sommario controllo a mente della loro validità richiedevano un certo tempo nel mentre sussisteva il pericolo che nell’intervallo intercorrente tra l’una e l’altra la stadia fosse stata mossa rendendo inutilizzabile la battuta in corso. Ecco i trucchi escogitati per risolvere il problema. Innanzitutto, anziché effettuare una lettura casuale come quella presa per esempio, si curava di far coincidere il filo inferiore esattamente con 1,00 metri della stadia ottenendo i seguenti notevoli vantaggi.
1) Eliminazione del primo numero da leggere, da ricordare e da trascrivere nel libretto:
2) Lettura immediata della distanza inclinata rendendo inutile l’esecuzione della successiva operazione di sottrazione tra i due valori dei reticoli estremi;
3) Possibilità di ricordare a memoria l’intera battuta del punto in quanto composta da due soli numeri e cioè la distanza inclinata ed il filo medio, e quindi di liberare immediatamente il canneggiatore dandogli modo di spostarsi quanto prima nel nuovo punto;
4) Verificare se al momento delle letture la stadia fosse realmente ferma ed il filo inferiore sempre posizionato esattamente su 1.00, provvedendo in caso contrario a riportarvelo con la vite dei piccoli spostamenti verticali.
5) Verificare l’assenza di errori di lettura tramite una facile operazione mnemonica.
La lettura riportata prima come esempio avrebbe avuto il seguente svolgimento.
Il filo inferiore, posizionato come di consuetudine a 1 metro, non richiedeva alcuna lettura. Il filo superiore andava a posizionarsi su m 1.40 rendendo estremamente facile ricavare e trascrivere direttamente la distanza inclinata cioè 40.00. L’unico filo il cui valore andava rilevato e trascritto normalmente era il filo medio (1.20 in questo caso). Il calcolo di verifica di corretta lettura poteva farsi molto semplicemente raddoppiando l’eccedenza rispetto a uno (20 * 2 = 40). In pratica, con la metodologia in oggetto non appena il canneggiatore aveva posizionato la stadia sul punto da rilevare, l’operatore in pochi secondi poteva fare la lettura dei due valori, e con un cenno al canneggiatore fargli capire che, essendo la lettura alla stadia ultimata, poteva spostarsi nel prossimo punto. Il completamento della battuta e cioè, in sequenza, la trascrizione nel libretto dei due dati e la lettura e trascrizione nel libretto dei valori angolari dei due cerchi potevano farsi successivamente e con tutta calma. Molto importante, ai fini di una buona restituzione, la breve descrizione delle caratteristiche di ciascun punto che riportavamo nel libretto di campagna. Il risultato finale era un rilievo molto veloce, preciso, compatibilmente con la strumentazione allora disponibile, in quanto comprensivo del controllo della inamovibilità della stadia durante la lettura e della verifica dei dati di stadia ed infine con l’indicazione della natura dei manufatti, della qualità del suolo e della sua conformazione. Si può dire che l’esecuzione del lavoro di campagna, contrariamente a quanto accade ai nostri giorni nei quali la semplificazione delle varie operazioni è così notevole da renderle più precise ma, al tempo stesso, banali, e,alla fin fine, noiose, richiedesse una grande partecipazione del topografo nell’utilizzare i trucchi del mestiere da renderla più interessante e piacevole. Da aggiungere a quanto già indicato il linguaggio a segni, oggi efficacemente sostituito da piccoli ma potenti apparecchi di trasmissione via radio, che veniva comunemente usato per comunicare a distanza col canneggiatore, il libretto di campagna, oggi sostituito da registrazione automatica dei dati, ed un tempo studiato per una facile loro scrittura a mano e per una rapida esecuzione dei calcoli a tavolino delle distanze e delle quote. La differenza con le moderne procedure diventa abissale quando si pensi ai moderni tacheometri che non richiedono nemmeno la presenza dell’operatore in quanto si orientano da soli sul segnale posto nel punto da rilevare ed eseguono automaticamente la lettura e la registrazione dei dati di campagna completi dei relativi commenti vocali. Tutto ciò senza voler accennare ad altri moderni sistemi di rilievo che si basano su tecnologie ancora pù avanzate e strabilianti come, ad esempio quelle relative alla fotogrammetria aerea o terreste o quello con collegamento a satelliti o a stazioni terrestri a speciale tecnologia.
Ma torniamo al nostro racconto della vecchia topografia.
Ultimato il lavoro di campagna aveva inizio la restituzione del rilievo per giungere al risultato finale e cioè al disegno della planimetria a curve ri livello e in scala adeguata.

 

 

 

A tale scopo occorreva innanzitutto completare la compilazione del libretto di campagna riportando negli spazi predisposti la distanza in proiezione orizzontale da stazione a punto battuto nonché la quota di quest’ultimo. Questa attività, a un certo punto, è stata facilitata dalla comparsa del regolo calcolatore speciale per topografia che consentiva di calcolare le ridotte in maniera rapida e precisa.

 

 

Anche per la messa in carta degli innumerevoli punti tramite gli elementi calcolati come detto e cioè per angolo e distanza dalla stazione, avevamo escogitato un metodo molto rapido e preciso. Innanzitutto ci eravamo costruiti e disegnato su carta lucida riproducibile dei rapportatori centesimali di grande diametro (il più grande aveva un metro di diametro) che fissavamo sul tavolo da disegno al di sotto del foglio trasparente su cui stavamo riportando il rilievo avendo cura di far coincidere il suo centro con la stazione ed orientandolo sulla base dei dati rilevati. A questo punto il rapportatore rappresentava esattamente sulla carta il tacheometro usato in campagna ed era possibile aprire per angolo e distanza tutte le battute fatte e riportare, a matita ed in scala opportuna, tutti i punti rilevati, ciascuno rappresentato con un circoletto e numero adiacente che indicava la relativa quota altimetrica. Tale operazione era facilitata da uno spillo infisso in corrispondenza del centro del rapportatore e da una tacca di riferimento fatta allo zero di una lunga riga centimetrata sulla quale avevamo riportato anche i valori nelle scale più usate.

 

 

Appoggiata la riga con la tacca sullo spillo, era sufficiente farla ruotare fino a leggere sul sottostante rapportatore visibile in trasparenza l’angolo
orizzontale di campagna e sulla riga la distanza orizzontale per poter tracciare via via tutti i punti.
Ultimato il posizionamento sulla carta di tutte le battute, aveva luogo il tracciamento, sempre a matita, delle curve di livello per interpolazione delle quote dei punti rilevati e il disegno del contorno dei vari manufatti il tutto sulla base delle descrizioni riportate nel libretto. L’elaborato finale su carta lucida riproducibile eliograficamente, era ottenuto ripassando il tutto con inchiostro di china nero. A proposito di eliografia vale la pena di ricordare come questo appellativo ed il chiaro riferimento alla luce del sole in esso presente, con cui si designa il più diffuso sistema di riproduzione dei disegni, derivi direttamente dal fatto che le prime riproduzioni dei lucidi venivano da noi fatte sfruttando la luce del sole alla quale esponevamo i nostri disegni dopo averli inseriti assieme alla carta sensibile in un telaio in legno con piano anteriore in vetro e con strettoio a vite che li teneva pressati tramite il pannello posteriore, anch’esso in legno.

 

 

La fine dell’esposizione era segnalata dal cambiamento di colore della carta sensibile, dal giallo intenso al bianco, cui faceva seguito lo sviluppo ad ammoniaca ottenuto introducendo e mantenendo la copia in elaborazione per una ventina di minuti in un cassone verticale e con apertura inferiore nel quale era contenuta la bottiglia dell’ammoniaca senza tappo di chiusura.
Interessante anche l’utilizzazione del “metodo dello spillo” già descritto per svolgere un’operazione, allora di difficile attuazione, come quella di ridurre o ingrandire, naturalmente in scala, dei disegni geometrici. A tale scopo, fissato il disegno al tavolo (senza rapportatore) e lo spillo sia all’interno sia all’esterno della figura da elaborare a seconda della ubicazione desiderata della nuova immagine da tracciare, era sufficiente orientare la riga, tenuta rigorosamente con la tacca sullo spillo, ad un punto caratteristico del disegno, leggervi, nella scala appropriata, la distanza polare dallo spillo e quindi, senza muovere la riga, tracciare il corrispondente punto semplicemente adottando sulla riga medesima tale distanza ma letta nella nuova scala. Passando via via di punto in punto era possibile e relativamente veloce, ricostruire l’intera figura nella nuova scala.

In tema di attrezzatura da usarsi negli anni in argomento non si può esimersi dal citare il planimetro cioè quello strumento a polo fisso che, facendo percorrere con il cursore a punta il contorno di una figura disegnata in scala, consentiva di determinarne l’area. E’ da rilevare come le superfici dei terreni che ancora oggi figurano nei registri castastali, siano state determinate con uno strumento rudimentale come quello rappresentato nella foto percorrendo a mano i confini di tutte le particelle sulla mappa scala 1:2000!

 

 

8) LA TRIANGOLAZIONE

Tra le opere più importanti realizzate nel dopoguerra figurano al primo posto gli impianti idroelettrici nel mentre per la loro realizzazione risultava di estrema importanza la topografia in quanto da essa dipendeva direttamente la buona riuscita delle imponenti opere di cui gli impianti stessi erano costituiti. Allo scopo era necessario disseminare in tutto il territorio interessato dai lavori, dei punti chiaramente ed esattamente individuabili i quali potessero costituire i riferimenti planimetrici di tutte le opere. Ad esempio dovendo costruire una galleria, lunga qualche decina di chilometri e munita di alcune finestre per accedervi in diversi punti lungo il suo percorso, era necessario avere in prossimità di ciascun imbocco dei punti di coordinate note dai quali poter determinare il punto di inizio e la esatta direzione di ogni tronco.
Importante innanzitutto la scelta dei punti trigonometrici i quali, oltre ad essere ubicati in prossimità di tutte le opere da tracciare e quindi disseminati in tutto il territorio, dovevano costituire i vertici di una maglia di triangoli che desse il risultato migliore in considerazione del fatto che le successive determinazioni erano basate esclusivamente su misure angolari.

 

 

I triangoli della maglia dovevano quindi avvicinarsi il più possibile alla forma equilatera e costituire, intersecandosi due a due, dei quadrilateri che ne agevolavano la compensazione chiamati cassoni.
Il compito non era affatto agevole visto e considerato che, essendo gli impianti idroelettrici di cui si parla ubicati in zone montagnose, per consentirne la visibilità reciproca i punti dovevano essere ubicati sulle cime delle alture o comunque in zone prive di ostacoli come alberature o manufatti.

 

 

 

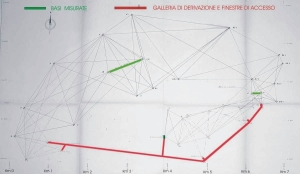
Fissati i punti ed individuati con apposite mire in legno dipinte di bianco e completata la misura delle due basi con le modalità già indicate, aveva luogo la lettura degli angoli nonché il calcolo delle coordinate applicando le regole della trigonometria piana e le relative compensazioni degli angoli e dei lati.
Come già detto i risultati erano ottimi. I lati dei triangoli e dei quadrilateri, determinati in doppio modo differivano tra di loro di pochi centimetri nel mentre il controllo definitivo consistente nella lunghezza
della seconda base dava una differenza contenuta entro i 10 cm.
La elevata precisione delle triangolazioni, come si evince dalla descrizione, era dovuta non tanto alle compensazioni fatte a tavolino o a particolari modalità di calcolo che, al contrario, erano fondate sulle elementari formule della trigonometria piana, quanto invece alla elevatissima qualità dei dati di campagna e cioé dalla rigorosa misura della distanza delle basi ed alla elevatissima precisione degli angoli misurati. Ai nostri giorni esistono sofisticati programmi di calcolo che tengono conto di mille circostanze, che effettuano un rigoroso trattamento degli errori di chiusura per dare il migliore risultato finale. Io ho fondati motivi per affermare che nulla può nella realtà sostituirsi alla cura che nei tempi andati veniva posta nella esecuzione del lavoro topografico condotto con le modalità indicate. Il tutto é comprovato dai risultati reali cui si perveniva. Era sopratutto nella costruzione delle gallerie degli impianti idroelettrici e precisamente nel momento di “foratura” di due tronchi lunghi svariati chilometri i cui fronti di scavo procedevano nel sottosuolo alla cieca l’uno verso l’altro fino a combaciare perfettamente, che aveva luogo la spettacolare dimostrazione della alta qualità del lavoro topografico! Il tutto tanto più ammirevole in quanto condotto utilizzando apparecchi rudimentali come quelli indicati!
Il giorno della foratura culminava con una grande festa con la quale si premiavano tutti coloro che avevano contribuito al raggiungimento dell’importante risultato tra i quali, ovviamente, l’esecutore materiale del lavoro topografico che tanta parte aveva avuto in esso. E’ opportuno rilevare come, vista l’importanza del lavoro topografico relativo alla costruzione delle gallerie, si usava eseguire un ulteriore importante controllo riguardante la loro direzione planimetrica. Esso aveva luogo mediante il così detto poligono esterno che consisteva nella esecuzione di una poligonale di collegamento di tutti gli imbocchi di una stessa galleria. Si trattava di una poligonale a lati molto lunghi dei quali venivano misurati solo gli angoli e pertanto, come già detto, era possibile controllare soltanto la direzione angolare del primo tronco di galleria. Si trattava, comunque, di un elemento importante che veniva controllato con una procedura a se stante e quindi valida.

 

9) LA LIVELLAZIONE TRIGONOMETRICA

Nella esecuzione della triangolazione di cui al precedente cap. 8) venivano letti, con la cura descritta, anche gli angoli del cerchio verticale il che consentiva, tramite l’applicazione di apposite formule e coefficienti che tenevano conto sia pure in maniera approssimativa della rifrazione e della sfericità terreste, di determinare le quote altimetriche dei punti trigonometrici. Quest’ultime, essendo basate su battute molto lunghe e per di più soggette alle citate approssimazioni, non erano esatte ma servivano quale importantissima verifica dell’assenza di errori grossolani nella livellazione geometrica di precisione già descritta al cap. 3).

 

10) IL TRACCIATO DELLE DIGHE AD ARCO CUPOLA

Assieme a quello delle gallerie era quello in oggetto il tracciato più spettacolare per il topografo.
Anche in questo frangente la carenza più sentita era l’impossibilità di effettuare, con la necessaria precisione, la misura delle distanze, elemento essenziale per materializzare ogni mattina i molti punti che occorreva fornire ai carpentieri perché potessero predisporre le casserature del getto.
Il problema venne risolto usando, anche in questo caso, le sole misure angolari e cioé tracciando ciascun punto per intersezione diretta delle visuali di due teodoliti in stazione contemporanea su due pilastrini anticipatamente predisposti al di fuori della zona di lavoro vera e propria.
Oltre ai pilastrini, scelti in modo che tutta l’opera fosse visibile da almeno due di essi, e definiti nello spazio tramite triangolazione, occorreva predisporre le coordinate di tutti gli elementi da tracciare e calcolati analiticamente sviluppando le equazioni matematiche fornite dai progettisti e che davano, in funzione della quota, gli angoli al centro, i raggi di curvatura e le coordinate dei centri relativi alla diga stessa e riferiti alla prefissata rete trigonometrica. In pratica il contorno dell’opera veniva definito nello spazio dalle coordinate di una serie di punti scelti per strati orizzontali ad equidistanza di 2 m corrispondenti all’altezza di ogni getto di calcestruzzo, nel mentre, per poterli materializzare, i punti stessi venivano riferiti ai pilastrini esistenti e di coordinate note tramite le sole direzioni azimutali.

 

i intuisce chiaramente come si trattasse di una enorme quantità di elementi analitici da calcolare utilizzando le modeste attrezzature allora disponibili, praticamente i soli logaritmi e i logaritmi delle funzioni trigonometriche e, più tardi, i valori naturali delle funzioni trigonometriche e la calcolatrice meccanica a mano. Nonostante tutte le difficoltà chi visitava il cantiere poteva vedere che di primo mattino, come si aprivano i lavori, in pochi minuti il canneggiatore osservando alternativamente lo strumento di destra e quello di sinistra piazzava sul calcestruzzo precedentemente gettato la serie di chiodini che definivano la posizione del bordo superiore della nuova casseratura.
Anche questo capitolo non può concludersi senza far rilevare l’enorme facilitazione resa possibile, riguardo le operazioni topografiche che ne formano oggetto, dalla moderna tecnologia. Da citare, oltre ai moderni distanziometri, l’uso del CAD che permetterebbe di saltare a pie pari tutti i calcoli analitici.
In pratica i profili e le piante alle diverse quote della diga potrebbero essere tracciate direttamente sul display del computer e, partendo direttamente dalle equazioni fornite dei progettisti, si potrebbero disegnare, sempre a video, i punti di dettaglio e quindi leggere direttamente i riferimenti ai pilastrini, cioé le aperture da strumento a punto per angolo e distanza atti al tracciamento di cantiere con operatore unico.

 

11) I CALCOLI TOPOGRAFICI

I mezzi a disposizione nei primi tempi, come già detto, erano esclusivamente i logaritmi dei numeri e delle funzioni trigonometriche che, non esistendo calcolatrici di sorta, facilitavano l’esecuzione delle operazioni di calcolo necessariamente fatte a mano. E’ ben noto come, tramite i logaritmi, vengano operate delle importanti semplificazioni delle procedure: le moltiplicazioni sono trasformate in somme, le divisioni in sottrazioni, le elevazioni a potenza in moltiplicazioni e così via.
Anche la determinazione delle funzioni trigonometriche non era tanto agevole dovendo essere fatta utilizzando le tavole.

 

 

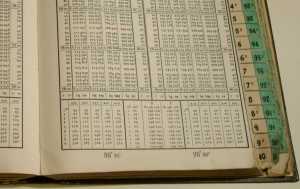
Tale determinazione era facilitata dalle apposite tabelline di interpolazione riportate in calce di ogni pagina, l’operazione era comunque macchinosa e fonte di possibili di errori. Ad un certo punto apparvero le prime calcolatrici meccaniche che permisero di abbandonare i logaritmi ed usare direttamente i valori naturali delle funzioni trigonometriche anch’esse calcolate tramite le apposite tabelle e con interpolazione effettuata come già spiegato.
Una delle calcolatrici più diffuse era la Brunsviga con la quale era possibile eseguire, sia pure con una certa manualità, le quattro operazioni fondamentali e perfino, con una procedura più complicata, la radice quadrata. Il balzo in avanti era già notevole ma lo é stato ancora di più quando é arrivata una macchina tanto straordinaria da meritare qui una menzione particolare: la Brunsviga doppia. Era composta da due calcolatrici manuali del tutto analoghe a quella prima descritta abbinate tra di loro e che potevano funzionare sia girando ambedue nello spesso senso o nel senso contrario l’una rispetto all’altra a seconda della impostazione data dall’operatore nel mentre il contatore meccanico o numeratore che dir si voglia, era unico.

 

 

 

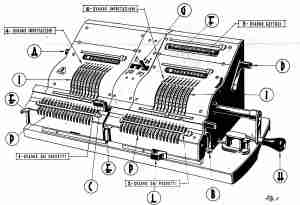
In pratica la calcolatrice doppia era in grado di effettuare contemporaneamente due operazioni di somma, sottrazione, moltiplicazione o divisione, in funzione di un unico numeratore. Ad esempio si poteva moltiplicare, con una unica operazione, per 43 sia il numero 520 che il numero 88 ottenendo nei due registri (quadri dei prodotti) i due risultati rispettivamente 22360 e 3784. Ma la cosa straordinaria era rappresentata dal fatto che una volta opportunamente impostate le due calcolatrici abbinate, era possibile, agendo sul carrello e sulla manovella di rotazione che ne costituivano i principali strumenti di utilizzazione, ricercare quella soluzione che dava, per ambedue le formule impostate, un unico risultato consentendo così di risolvere, in maniera semplice, problemi matematici che avrebbero, con le normali calcolatrici allora in uso, richiesto complicatissime procedure. Ciò poteva aver luogo ogni qualvolta esistevano, come in matematica o in geometria accade assai frequentemente, due diverse formule che, partendo da dati diversi, portavano al medesimo risultato. Si trattava in qualche modo di precorrere i tempi e cioè di una rudimentale applicazione del calcolo iterativo, comunemente usato nei moderni computer.
Come noto, ai nostri giorni, quando siamo in presenza di problemi particolarmente difficili da risolvere, si ricorre alla iterazione che consiste nell’iniziare il calcolo con una procedura approssimata e quindi affinare via via il risultato, sempre con procedure approssimate ma semplici. Ad ogni iterazione il computer confronta automaticamente il nuovo risultato con quello precedente sospendendo le iterazioni non appena la differenza riscontrata rientra entro le tolleranze ammesse. Allo stesso modo con la calcolatrice doppia il risultato veniva via via affinato fino ad ottenere, con la equiparazione di quello dell’una a quello dell’altra macchina che funzionava in parallelo o in senso contrario, la risoluzione definitiva di problemi matematici complessi. Non si ritiene opportuno in questa sede descriverne in dettaglio le procedure, data la difficoltà che vi si incontrerebbe. Ci si limita ad indicare come, nella realtà, fossero in grado di dare, tenuto conto dei tempi di cui si discorre ed una volta imparate, velocità nei calcoli prima giudicate impensabili. In ognuna delle due calcolatrici abbinate bisognava impostare i dati di una formula atta a dare il medesimo risultato fatta salva la necessità di tener conto dei segni matematici di ogni elemento mediante la regolazione del senso di rotazione dell’una macchina rispetto all’altra e del senso di rotazione assoluto della manovella. Il tutto era codificato dalle regole precise del libretto di istruzioni che veniva fornito, in copia eliografica di un lucido redatto a mano libera, assieme alla macchina e di cui si riporta, per darne un’idea di massima, un breve estratto nella figura 23 relativa alla esecuzione di calcoli topografici. Quanto sopra può dare un’idea delle reali difficoltà che si incontravano allora nella esecuzione di calcoli oggi resi estremamente facili dai mezzi di calcolo di cui si può facilmente disporre.

 

12) CONCLUSIONI

Sono state descritte alcune delle procedure che un tempo venivano comunemente utilizzate nelle operazioni topografiche per poter ottenere gli stessi risultati che oggi si hanno in maniera notevolmente più semplice grazie alle attrezzature disponibili sia come strumentazione di campagna e sia in quelle di restituzione a tavolino. Viene posta in risalto la grande partecipazione che allora era richiesta nell’esecuzione di operazioni che, con la moderna attrezzatura, sono superate e sostituite dagli automatismi rendendo il compito estremamente semplice e, in definitiva, meno interessante.

aggiornamento: agosto 2006